Reglo ICC serial port control via Matlab

Posted on April 15, 2016 by P.T.R. Rupprecht

For my experiments with zebrafish, I typically generate dynamic odor landscapes for the fish / fish brain explant by varying the speed of the wheels of an Ismatec peristaltic pump, thereby changing the concentration of the applied stimuli over time. Recently, I bought one of their digital pumps (Reglo ICC with four independent channels), but the company only provides a Labview code sample for custom implementation.

I wrote a small Matlab adapter class to interface with the pump. In order to spare other people from this effort, here is my implementation on Github. It allows to change pump speed, pumping direction etc by a serial protocol that is transmitted via USB and a virtual COM port. – It should be easy to use this as a starting point for a similar code snippet in Python.

Clearly, this will be useful for only a small number of people, but I at least would have been glad to find a sample code in the internet that could have spared me the time to write the code by myself. Hopefully Google will find its way to direct people in need to these links. Here are some guiding tags: Reglo ICC, Ismatec, Cole-Parmer, serial port, USB, COM, serial object, adapter class, object-oriented Matlab.

Posted in Uncategorized | Tagged , , , , , | 13 Comments

Fast z-scanning using a voice coil motor

Posted on April 6, 2016 by P.T.R. Rupprecht

We just published a paper on fast remote z-scanning using a voice coil motor. For 2P calcium imaging. It’s a nice paper with some interesting technical details.

The starting point was the remote z-scanning scheme used by Botcherby et al. (2012) from Tony Wilson’s lab, but we modified the setup to make it easier to implement for an existing standard 2P microscope, and we used only off-the-shelf components, for in total <2500 Eur.

The first challenge when implementing the Tony Wilson remote scanning scheme was to find something that can move a mirror in axial direction with high speed (sawtooth, >5 Hz). Botcherby et al. used a costum-built system consisting of a metal band glued to synchronized galvos. In order to simplify things (for details on optics etc, see the paper), I was looking for a device that comes off-the-shelf and that can move fast in a linear way over a couple of millimeters. That is, a very fast linear motor. Typical linear motors are way too slow (think of a typical slow microscope stage motor).

End of 2014, I found a candidate for such a linear motor: loudspeakers. When you have a close look at large subwoofers, you can see that the membranes move over many millimeters in extreme cases; and such loudspeakers are used for operation between 20 Hz and 10 kHz, so they are definitely fast. So I bought a simple loudspeaker for 8 Euro and glued a mirror onto the membrane. However, precision in the very low frequency domain (< 50 Hz) was limited, at least for the model I had bought:

loudspeaker

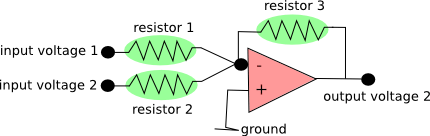
But as you can see, this is a very simple device: A permanent magnet and two voltage input pins, nothing else. Ok, there is the coil that is attached to the backside of the membrane, but it remains very simple. The copper coil is permeated by magnetic field and therefore experiences a force when electrical current flows through the coil, thereby inducing motion of the coil and the attached membrane.

In spring 2015, I realized that the working principle of such loudspeakers is called “moving coil” or ” voice coil”, and using this search term I found some suppliers of voice coil motors for industrial applications. These applications range from high repeatability positioning devices (such as old-fashioned, non-SSD hard drives) to linear motors working at >1000 Hz with high force to mill a metal surface very smoothly.

So, after digging through some company websites, I bought such a voice coil motor together with a servo driver and tried out the wiring, the control and so on. It turned out to be such a robust device that it is almost impossible to destroy it. I was delighted to see this, since I knew how sensitive piezos can be e.g. when you push or pull into a direction that does not convene to the growth direction of the piezo crystal.

This is how the voice coil motor movement looks like in reality inside of the setup. I didn’t want to disassemble the setup, so it is here within the microscope. To make the movements visible for the eye, it is scanning very slowly (3 Hz). On top of the voice coil motor, I’ve glued the position hall sensor (ca. 100 Euro). I actually used tape and wires to fix the positions sensor – low-tech for high-precision results.

The large movement of the attached mirror is de-magnified to small movements of the focus in the sample, thereby reducing any positional noise of the voice coil motor. This is also the reason why I didn’t care so much about fixing the hall sensor in a more professional way.

After realizing that it is possible to control the voice coil motor with the desired precision, repeatability and speed, it remained to consider more closely the optics of the remote scanning system. Actually, more than two third of the time that I spent for this paper were related to linear ABCD optics calculations, PSF measurements and other tests of several different optical configurations, rather than being related to the voice coil motor itself.

More generally, I think that voice coil motors could be interesting devices for a lot of positioning tasks in microscopy. The only problem: To my knowledge, typical providers of voice coil motors have rather industrial applications in mind, which reduces the accessibility of the technique for a normal research lab. A big producer of voice coil motors is SMAC, but they seem to have customers that want to buy some thousand pieces for an industrial assembly line. I prefered both the customer support and the website of Geeplus and I bought my voice coil motor from this company – my recommendation.
As described in the paper, I used an externally attached simple position sensor system, but there are voice coil motor systems that have an integrated encoder. Companies that sell such integrated systems are Akribis Systems and Equipsolution, and our lab plans to have a try with those (mainly because of curiosity). Those solutions use optical position sensors with encoders instead of a mechanical hall sensors, increasing precision and lowering the moving mass, but also at higher cost.
One problem with some of these companies is that they are – different from Thorlabs or similar providers – not targeted towards researchers, and I found it sometimes difficult or impossible to get the information I needed (e.g. step response time etc.). If I were to go for a voice coil motor project without previous experience, I would either go the hard way and just buy one motor plus driver that look fine (together, this can easily be <1000 Euro, that is, not much) and try out; or stick to the solution I provided in the paper and use it as a starting point; or ask an electrical engineer who knows his job to look through some data sheets and select the voice coil motor that you want to have for you. I did it the hard way, and it worked out for me in a very short time. Me = physics degree, but not so much into electronics. I hope this encourages others to try out similar projects themselves!

During the review process of the paper, one of the reviewers pointed out a small recent paper that actually uses a regular loudspeaker for a similar task (field shaping). This task required only smaller linear movements, but it’s still interesting to see that the original idea of using a loudspeaker can somehow work.

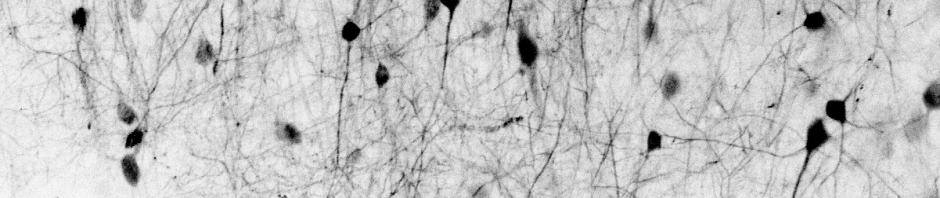
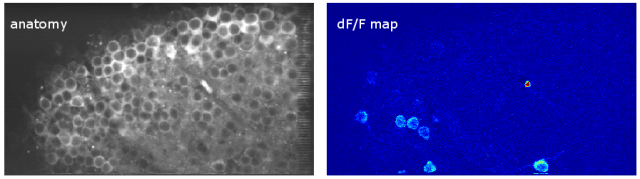
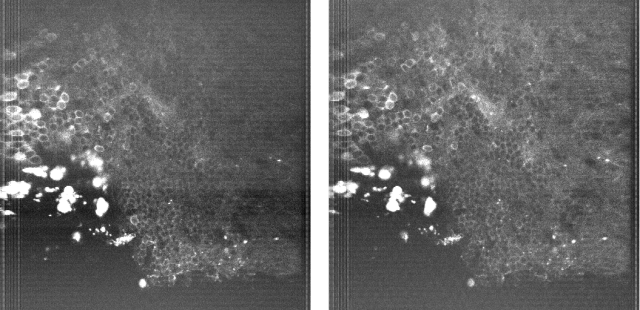
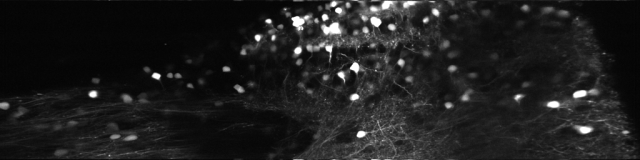
Since then, I’ve been using the voice coil motor routinely for 3D calcium imaging in adult zebrafish. Here is just a random example of a very small volume, somewhere in a GCamped brain, responding to odor stimuli. Five 512 x 256 planes scanned at 10 Hz. The movie is not raw data, but smoothed in time. The movies selected for the paper are of course nicer, and the paper is also open access, so check it out.

 

 

Posted in Calcium Imaging, Imaging, Microscopy, Neuronal activity | Tagged , , , | 3 Comments

Modulating laser intensity on multiple timescales (x, y and z)

Posted on March 25, 2016 by P.T.R. Rupprecht

In point-scanning microscopy and especially when using resonant scanners, the intensity of the beam is typically modulated using a Pockels cell. For resonant scanning, the dwell time per micrometer is not constant along the scanned line, and one wants either to modulate the laser intensity accordingly (here’s an example) or at least shut down the laser beam at the turnaround points, where the velocity of the scanner is basically zero for some microseconds. A command signal to shut down the laser for this period could look similar to this one on a noise oscilloscope, with the dips representing the laser beam blanking during the turnaround points:

LineDip

However, sometimes the tissue is illuminated inhomogeneously, and it would be nice to increase the laser power when scanning the dim parts of the FOV. For example, in the adult zebrafish brain that I’m working with, the bottom of the FOV can be at the bright surface of the tissue, whereas the top of the image is dim due to its depth below some scattering layers of gray matter. In order to compensate for this inhomogeneity, I wanted to be able to modulate the pockels cell both in x, y, and at the turnarounds (x-direction). The problem is purely technical: In order to create a driving signal for the pockels cell on these two timescales (less than microseconds and more than milliseconds), one needs high temporal resolution and a long signal ( a long “waveform” in LabView speak). However, a typical NI DAQ board’s onboard memory is limited to 8192 data points. Which makes it impossible to modulate intensity in x and y.

I used a very simple solution to work around this problem. The idea is to generate two separate signals for modulation in x and y and then simply add the two output voltages. This does not allow for arbitrary 2D modulation patterns, but typically I’m happy with a linear combination of x- and y-modulation.
This solution disregards the non-linearity of a typical sine-shaped pockels cell calibration (input voltage vs. output laser intensity), but as long as the result is better than before, why not do it? This is what comes out:

ModulationExample

Note that the timescale is 25 microseconds on the left-hand side, and 25 milliseconds on the right-hand side.

The only technical challenge that I had to deal with was the following: From the DAQ boards, I get two separate voltage outputs. How do I sum them up? Of course, one can buy an expensive device that can do this and many other things by default. Or, one can build a summing amplifier, for less than 10 Euro:

summingAmplifier

Here is a description of this very simple circuit. Just use three equal resistors (labeled green), and you have an (inverting) unity gain voltage summer. In order to maintain the temporal precision, use a MHz operational amplifier (labeled red above). I bought this one for < 1 Euro. It took me less than 30 min with a soldering gun to assemble the summing amplifier, so it’s pretty easy. That’s how it looks like in reality, with an additional zoom-in of the core circuit:

summingAmp

And here is a small random brain region expressing GCaMP before (left) and after (right) the additional modulation in x and y:

BrainBoth

The average power is the same. The closer I looked, the more substantial the difference got. For example, the bright dura cells on the left are really annoying due to their brightness, but less so in the right-hand side image. I was surprised myself by how much this small feature improves imaging in curved brain regions, given the little money and effort it demanded.

Also, it is apparently straightforward to extend the y-direction modulation into a modulation in y and z, since the two timescales are similar (30-60 Hz framerate vs. 5-15 Hz volume rate for my experiments).

Posted in Calcium Imaging, Imaging, Microscopy | Tagged , , , | 1 Comment

Deep learning, part III: understanding the black box

Posted on February 27, 2016 by P.T.R. Rupprecht

As many neuroscientists, I’m also interested in artificial neural networks and am curious about deep learning networks. I want to dedicate some blog posts to this topic, in order to 1) approach deep learning from the stupid neuroscientist’s perspective and 2) to get a feeling of what deep networks can and can not do. Part I, Part II, Part IV, Part IVb. [Also check out this blog post on feature visualization; and I can recommend this review article.]

The main asset of deep convolutional neural networks (CNNs) is their performance; their main disadvantage is that they can be used with profit, but not really understood. Even very basic questions like ‘why do we use rectified linear units (RELUs) as activation functions instead of slightly smoothed versions?’ are not really understood. Additionally, after learning the network is a black box that performs exceedingly well, but one cannot see why. Or, it performs badly, and also to sometimes cryptic reasons. What has the network learned actually?

But there are some approaches that shed light on what has been learnt be CNNs. For example, there is a paper by Matthew Zeiler. I’ve mentioned a Youtube-Video by him in a previous post (link to video). He uses a de-convolution (so to say, a reverse convolution) algorithm to infer the preferred activation pattern of ‘neurons’ somewhere in the network. For neurons of the first layer, he sees very simple patterns (e.g. edges), with the patterns getting more complex for intermediate (e.g. spirals) and higher layers (e.g. dog face). The parallels to the ventral visual stream in higher mammals is quite obvious.

Google DeepDream goes into the same direction, but yielding more fascinating pictures. Basically, the researchers took single ‘neurons’ (or a set of neurons encoding e.g. animals) in the network and used a search algorithm to find images that activate this ‘neuron’ most. The search algorithm can use random noise as a starting point, or an image provided by the user. Finally, this leads to the beautiful pictures that are well-known by now (link to some beautiful images). Google has also released the source code, but within the framework of Caffè (link), and not Tensorflow. However, at the bottom line of this website, they promise to provide a version for Tensorflow soon as well [Update October 2016: It has been released now].

In the meantime, let’s have a less elaborate, but more naïve look, in order to get a better understanding of deep networks. I will try to dissect parts of a 5-layer convolutional network that I wrote during the Tensorflow Udacity course mentioned previously in this blog. For training, it uses a MNIST-like data, but a little bit more difficult. The task is to assign a 28×28 px image to one of the letters A-J. Here you can see how the network performs for some random test data. In the bar plot, the positions 1-10 correspond to the letters A-J, visualizing the certainty of the network.

fig1

So let’s look inside the black box. The first layer in this network consists of sixteen 5×5 convolutional filters. Those filters had been established during learning. Here they are:

fig2

Does this make sense to you? If not, here are the 16 filters (repeatedly) applied to noise, revealing the structures that are made to detect:

fig3

Obviously, most of those filters have a preference for some (curved) edge elements (which is not really surprising).

For simple networks like this one, which is not very deep and only has to learn simple letters, intermediate layers do not really represent something fancy (like spirals, stars or eyes). But one can at least have a look at how the ‘representation’ of the fifth layer, the output layer looks like. For example, what is the preferred input pattern of the output ‘neuron’ that has learned to assign the letter ‘C’?

To find this out, I used the same deep learning network as before, but kept constant the network weights that had been learnt before. Instead, I varied the input image, whilst telling the stochastic gradient descent optimizer to maximize the output of the ‘C’ neuron.

Starting from random noise, different local optimization maxima are reached, each of them corresponding more or less to an ‘idea of C’ that the deep network has in mind. The left side shows ‘C’s from the original dataset. The right hand side shows ideas of ‘C’ that I extracted from the network with my (crude) search algorithm. One obvious observation is that the extracted ‘C’s do not care about surfaces, but rather about edges, which can be expected from a convolutional network and from the filters of the first layer shown above.

fig4

Posted in machine learning | Tagged , , | 4 Comments

Undistort/unwarp images for resonant scanning microscopy

Posted on February 16, 2016 by P.T.R. Rupprecht

For image acquisition using a resonant scanning microscope, one of the image axes is scanned non-linearly, following the natural sinusoidal movements of the resonant scanner. This leads to a distortion of the acquired images, unless a online correction algorithm or temporal non-homogeneous sampling rate is used. A typical (averaged) picture:

unnormal

Clearly, the left and right side of the picture are streched out. This does not worry me if I only want to extract fluoresence time courses of neuronal ROIs; but it is a problem for nice-looking pictures that want to have a valid scalebar. Unfortunately, I didn’t find any script in the internet on how un-distorting is normally being done for resonant scanning, so I want to present my own (Matlab) solution for other people looking around. It is not elegant, but it works. For the final solution, scroll to the bottom of the blog entry.

Continue reading →

Posted in Calcium Imaging, Microscopy | Tagged , , , , | 1 Comment

Deep learning, part II : frameworks & software

Posted on February 3, 2016 by P.T.R. Rupprecht

As many neuroscientists, I’m also interested in artificial neural networks and am curious about deep learning networks. I want to dedicate some blog posts to this topic, in order to 1) approach deep learning from the stupid neuroscientist’s perspective and 2) to get a feeling of what deep networks can and can not do. Part I, Part III, Part IV, Part IVb.

To work with deep learning networks, one can either write ones’s own functions and libraries for loss functions or backpropagation; or use one of the available “frameworks” that provide the libraries and everything else under the hood that is more interesting for developers, but not for users of deep learning networks.
Here’s a best of: Tensorflow, Theano, Torch, Caffe. Out of those, I would recommend either Tensorflow, the software developed and used by Google, and Theano, which is similar, but developed by academic researchers. Both can be imported as libraries in Python.

First, I tried to install both Theano and Tensorflow on Windows 7, and gave up after a while – both frameworks are not designed to work best on Windows, although there are solutions that do work (update early 2017: Tensorflow is now also available for Windows, although you have to take care to install the correct python version). So I switched to Linux (Mint) and installed Tensorflow, and spent some time digging out my Python knowledge that got lost during the last couple of years when I used Matlab only.

Here’s the recipe that should give a good handle on Tensorflow in 2-4 days:

  1. Installation of Tensorflow. As always with Python, this can easily take more than one hour. I installed a CPU-only version, since my GPU is not very powerful.
    .
  2. Some basic information to read – most of this applies to Theano as well.
    .
  3. Then here’s a nice MNIST tutorial using Tensorflow. MNIST is a standard number recognition dataset that is used as a standard benchmark for supervised classifiers.
    .
  4. For a more systematic introduction, check out the Tensorflow udacity class that has been announced recently on Google’s research blog, based on a dataset similar to MNIST, but a little bit more difficult to classify. The lecture videos are short and focused on a pragmatic understanding of the software and of deep learning. For deeper understanding, please read a book.
    .
    The core of the Tensorflow class is the hands-on part which consists of code notebooks that are made available on github (notebooks 1-4). This allows to understand the Tensorflow syntax and solve some “problems” by modifying small parts of the given sample code. This is really helpful, because googling for possible solutions to problems gives a broader overview of Tensorflow. Going through these exercises will take 1-3 days of work, depending on whether you are a perfectionist or not.
    .
  5. Now you should be prepared to use convolutions, max pooling, dropout and stochastic gradient descent on your own data with Tensorflow. I will try do to this in the next couple of weeks and report it here.

Here are some observations that I made when trying out Tensorflow:

  1. There are a lot of hyperparameters (learning rate, number of layers, size of layers, scaling factor of L2 regularization of different layers, shape/stride/depth of convolutional filters) that have to be optimized. Sometimes the behavior is unexpected or even unstable. I didn’t find good and reliable advice on how to set the hyperparameters in function of the classification task.
    .
  2. To illustrate the unpredictable behavior, here is a very small parameter study on a neural network (no convolutional layer) with two hidden layers with 50 and 25 units each. The factors L1 and L2 give the scaling of the L2 regularization loss term (for explanation see chapter 7.1.1 in this book) of the respective layers. If the loss function for the (smaller) second hidden layer is weighted more strongly than the loss function for the first hidden layer (i.e., L2 >> L1), the system is likely to become unstable and to settle to random assignment of the ten available categories (= 10% success rate). However, whether this happens or not depends also on the learning rate – and even on the initialization of the network.
    .

    L1\L2 1e-4 5e-4 1e-3 5e-3
    1e-4  89.9%  10.0%  10.0%  10.0%
    5e-4  91.8%  91.9%  92.1%  10.0%
    1e-3  92.3%  92.6%  92.2%  10.0%
    5e-3  10.0%  10.0% 89.3%  10.0%

    .

  3. When following the tutorial and the course, there is not much to be done except for tweaking algorithms and hyperparameters, with the only network performance readout being “89.1%”, “91.0%”,”95.2%”,”10.0%”,”88.5%” and so on; or maybe a learning curve. It’s a black box with some tunable knobs. But what has happened to the network? How did it learn? How does its internal representation look like? In one of the following weeks, I will have a look into that.
Posted in machine learning | Tagged , | 3 Comments

Deep learning, part I

Posted on January 27, 2016 by P.T.R. Rupprecht


As many neuroscientists, I’m also interested in artificial neural networks and am curious about deep learning networks, which have gained a lot of public attention in the last couple of years. I’m not very familiar with machine learning, but I want to dedicate some blog posts to this topic, in order to 1) approach deep learning from the stupid neuroscientist’s perspective and 2) to get a feeling of what deep networks can and can not do. (Part II, Part III, Part IV, Part IVb.)

As a starter, here’s my guide on how to start with deep (convolutional) networks:

  1. Read through the post on the Google Research blog on Inceptionism/DeepDreams which went viral mid of 2015. The authors use deep convolutional networks that were trained on an image classification task and encouraged the networks to see meaningful structures in random pictures.
    .
  2. Check out this video talk given by the head of DeepMinds Technologies @ Google, showing the performance of one deep learning network playing several different Atari video games. He talks about AGI, artifical general intelligence, “solving intelligence” and similar topics. Not very deep, but maybe inspirational.
    .
  3. If you do not know what convolutions are, have a look at this post on colah’s blog. If you like this post, consider exploring the rest of this blog – it is well-written throughout, trying to avoid any terms that are used by machine learning people or mathematicians only.
    .
  4. Take your time (45 min) and watch this talk about visualizing and understanding deep neural networks. Different from many explanatory videos, this one gives an idea in which terms (network architecture, computational costs, benchmarks, competition between research group) those people think.
    .
  5. Read the original research paper associated with Google’s DeepDream. Search for any methodological part of the paper you have not heard of before.
    .
  6. Find out about not purely feedforward network components, e.g. Long Short Term Memory (LSTM) to broaden your understanding: Colah’s blog or wikipedia.
    .
  7. You want to better understand some parts (or everything)? Go read this excellent, still unpublished, freely available book on deep learning, especially Part II. Also for people that do not use math every day, it is still not difficult to understand.
    .

(That’s roughly the way I went: hope that helps others, too.)

Now one should be prepared to answer most of the following questions. If not, maybe you want to find out the answers by yourself:

  • What is so deep about deep convolutional neural networks (CNN)?
    .
  • What is a typical task of such CNNs and how are they typically benchmarked?
    .
  • What is a convolution?
    .
  • How do typical convolutional filters for CNNs designed for image classification look like? Are they learned or manually chosen?
    .
  • Why are different layers used (convolutional layers, 1×1 convolutional layers, pooling layers, fully connected layers) and what are their respective tasks?
    ..
  • Is a deep CNN always better when it is bigger? (Better in terms of classification performance.)
    .
  • How does learning occur? How long does it take for high-end networks? Minutes, weeks, years? Which hardware is used for the learning phase?
    .
  • Which layers are computationally expensive during learning? Why?
    .
  • What are rectified linear units, where and why are they used?
    .
  • What role does the cost function play during learning?
    .
  • Why is regularization used in the context of learning? What is it?
    .
  • How can a CNN create pictures like in Google’s DeepDream? Does it require any further software/programming except for the CNN itself?
    .

Now, with a rough understanding of the methods and concepts, it will be time to try out some real code. I hope I’ll have some time for this in the days to come and be able to post about my progress.

Posted in machine learning | Tagged , , , , | 3 Comments

Point spread functions

Posted on December 14, 2015 by P.T.R. Rupprecht

One way to characterize the quality of one’s microscope is to measure the point spread function (PSF), that is the image that is created by a point source  (which can be a fluorescent bead smaller than the expected size of the PSF embedded in agarose). I recently spent quite some time aligning my multiphoton microscope, and due to some reasons, it took me not only some hours, but several days (or nights). In the end, the PSF again was symmetric, small, sharp and nice, but the way to go there was crowded with all varieties of bad, strange and extremely ugly PSFs, sometimes at points during the alignment when I didn’t expect it.

In scientific publications, one only gets to see the nicest symmetric ‘typical’ PSFs, so I just want to put some really bad PSFs here. Not all the PSFs were as bad as they look like, because I have adjusted the contrast of the gifs in order to better show the shape of the PSF. All gifs are simple z-stacks acquired with variable z-spacing at the same day on the very same microscope, with only minor and rarely predictable changes to the beam path.

Here comes the classical stone in the water-PSF, thrown from the lower right:

theCounterDrifter

This one is thrown from the top right:

theSaturnWithManyRings

This is the bathing in a sea of other beads-PSF. Or, rather than bathing, swimming, because there is a clearly visible upwards direction. This happens when you have to many beads in your agarose:

theSwimmerInASeaOfBeads

This astigmatic PSF, on the other hand, is rather indecisive, first going to the right and then upwards.

theUndeciciseWanderer2

Here an even more advanced indecisive right-up-goer-PSF:

theUndeciciseWanderer

This one is so undecided that it decides to almost split in two halves. Let’s call it the bifurcating PSF:

theAsymmetricHalo

This is the banana-PSF, coming from the left and going back again:

theHalfBanana

And finally, you would not guess this to be a PSF, here comes the flying eagle-PSF. I created it simply by tightening too much one of the screws that held the dichroic beam splitter, the back aperture of the objective still seemed to be properly filled:

theFlyingEagle_pressureOnDichroic

Amazing!

Sidenote: In some of these pictures in one or two planes, one can see a diagonal striping pattern. This comes from the pulsing laser, which was unstable during these days, being modulated to the microsecond-timescale. Fortunately, nowadays I have a nice PSF and a stable laser again …

Posted in Microscopy | Tagged , , | 4 Comments

Aphantasia

Posted on November 14, 2015 by P.T.R. Rupprecht

A couple of days ago, during a hiking tour close to Luzern, I met a medical doctor from Israel who decided to join me for my hike for the rest of the day. After some time, when I made fun of her taking so many pictures, she pointed out that she had a rare neurological condition that prevented her from recalling pictures and that she did not have a picture of anything in her mind when she closes the eyes.   Continue reading →

Posted in Uncategorized | Tagged , , | Leave a comment

EODs for kHz imaging

Posted on August 29, 2015 by P.T.R. Rupprecht

J. Schneider et al., and S. Hell recently published a paper on STED microscopy, using EODs (electro-optical deflectors) to scan 512 x 512 pixels at frame rates of 1000 Hz. Compared to AODs, EODs offer the costumer-friendly advantage of not dispersing the the spectral components of the laser beam. Their main weakness is a small deflection angle. In her thesis from 2012, Jale Schneider gives an overview of manufacturers of EODs:

Company deflection angle per kV [mrad] aperture [mm] capacity [pF]
Conoptics Inc. USA 7.8 2.5 180
NTT Photonics Laboratories, Japan 150 0.5 1000-2000
Leysop Ltd., GB 1.5 3 50
Leysop Ltd., GB 3 2 50
Leysop Ltd., GB 5 1 50
Quantum Technologies, USA 3.5 3 100
AdvR Inc., USA 24 < 0.8 < 100

For resonant scanning, the aperture is ~ 5 mm, the deflection angle 90-260 mrad (depending on resonant frequency).

The capacity of the crystal displayed in the table comes into play indirectly, with a smaller capacitance demanding less from the high-voltage driver system of the EOD. In the appendix of her thesis, Jale Schneider also gives an overview of commercial high-voltage driver systems, although for her work she custom-built one.

Maybe at some point, this will become interesting for voltage imaging in dendrites. Assume one could drive the Conoptics EOD with 5 kV, and let’s further assume a 60x objective (focal length of ca. 3 mm) and a scan lens/tube lens system with magnification 3x. Then one has a 7.5 mm diameter beam on the back focal plane, and a FOV in the sample of ca. (3 mm)/3*tan(5*0.0078 rad) = 40 μm. Such a system would be an alternative to the AOD-based approach, which was, for instance, used by Arthur Konnerth’s lab for kHz calcium imaging of dendritic spines (250 × 80 pixels, field of view = 28 × 9 μm, 40x objective).

[Update] It seems that this estimation is only approximately correct. As described in the thesis cited above, the Conoptics EOD can use the 2.5 mm aperture only for a non-deflected beam. It seems that even for a +- 7.2 mrad deflection, the maximum unclipped beam diameter is only 1.5 mm.

Posted in Uncategorized | Tagged , , , | Leave a comment